Are quintile scores numeric or factors?

[fcas80]

Hi. I have a dataset with various independent variables, and scores similar to credit scores as my dependent variable. The complication is that the scores are only given in quintiles, such as a score between 0 and 19 is given as a 1, 20 to 39 is given as a 2, etc. Do I treat these scores as numeric or as factors? Thank you.

[Yarnabrina]

My suggestion: ordered factor. Use factor and specify levels, or just set ordered as TRUE.

[technocrat]

I would rephrase the question: Is credit score as the dependent/response variable better treated as continuous or categorical? Is the goal prediction or classification?

[fcas80]

My goal is prediction.

As I understand it, regression will create dummy variables of a variable that is declared as a factor.

What is the effect of ordering the levels? Why does that matter in a regression? Does it matter in other algorithms?

[technocrat]

This is analogous to categorizing the scores into bins. The assumption of normality of residuals is violated.

# Load libraries
library(haven)

# Read in data
odata <- read_dta("https://stats.idre.ucla.edu/stat/data/ologit.dta")

# ols model with the single quantitative predictor

misfit <- lm(apply ~ gpa, data = odata)
summary(misfit)
#> 
#> Call:
#> lm(formula = apply ~ gpa, data = odata)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -0.7917 -0.5554 -0.3962  0.4786  1.6012 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)   
#> (Intercept) -0.22016    0.25224  -0.873  0.38329   
#> gpa          0.25681    0.08338   3.080  0.00221 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.6628 on 398 degrees of freedom
#> Multiple R-squared:  0.02328,    Adjusted R-squared:  0.02083 
#> F-statistic: 9.486 on 1 and 398 DF,  p-value: 0.002214

plot(misfit,2)

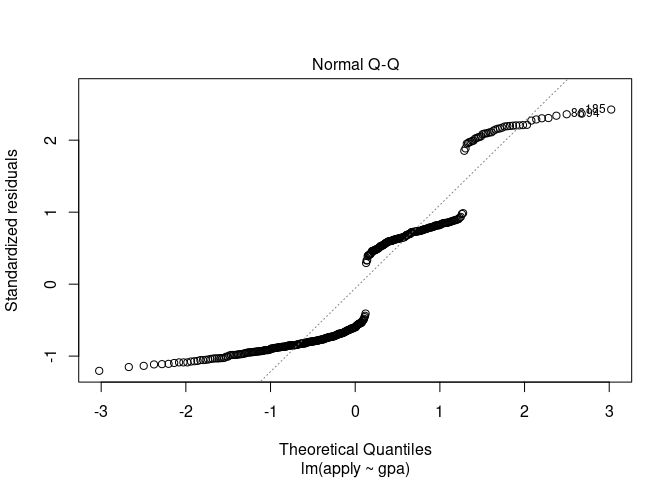
# changing response variable to a factor throws an error
odata$apply <- factor(odata$apply)
misfit <- lm(apply ~ gpa, data = odata)
#> Warning in model.response(mf, "numeric"): using type = "numeric" with a factor
#> response will be ignored
#> Warning in Ops.factor(y, z$residuals): '-' not meaningful for factors

[startz]

Why would normality of the errors matter with 400 obseravtions?

[technocrat]

Linear models assume that the response is continuous and the error has a normal distribution.

RDS §23.6

[startz]

Linear models do not necessarily assume the error has a normal distribution. For example, the Gauss-Markov theorem does not depend on the error distribution being normal.
Having a normal distribution matters for some things, although very few things if there are a large number of observations.

[technocrat]

You’re right on both counts, and I shouldn’t have overgeneralized. For purposes of queuing up a predictive analysis of an ordinal response I wanted to steer thinking away from OLS where the problems seem obvious.

[startz]

Yeah, getting the equation right is the most important thing. Couldn't agree more.

[Yarnabrina]

I was actually suggesting ordinal logistic model, not OLS. But may be there are other and possibly better alternatives as well.