Decision Tree and fancyrpartplot

[mdg202]

Hello,

Currently I am working on a decision tree model however some issues came up.

This is the current r chunk
model = rpart(loan_status ~ loan_amnt+age, data=dat2, method="class", control=rpart.control(minsplit=1, minbucket=1, cp=0.001))
fancyRpartPlot(model)

However i got the following error:
Error in apply(model$frame$yval2[, yval2per], 1, function(x) x[1 + x[1]]) : dim(X) must have a positive length

Attached is my data

[FJCC]

What do you get if you run

model = rpart(loan_status ~ loan_amnt+age, data=dat2, 
                method="class", 
                control=rpart.control(minsplit=1, minbucket=1, cp=0.001))

and then

summary(model)

[mdg202]

I got the following

[FJCC]

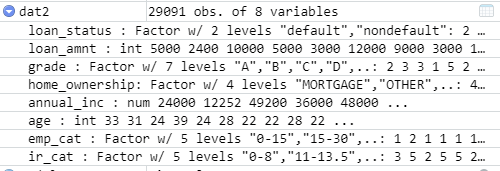
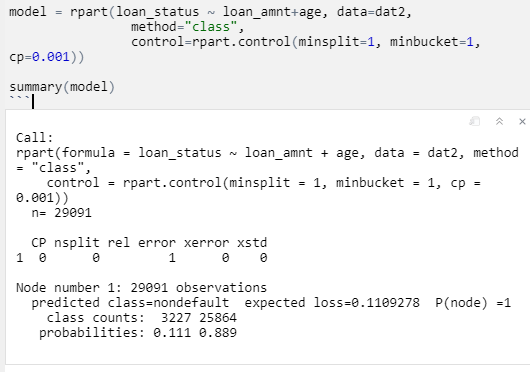
You are not getting any splitting. I have never used fancyRpartPlot but it seems it does not like model with no splits. Here is an example using a built-in data set showing what the summary should look like.

library(rpart)
#> Warning: package 'rpart' was built under R version 3.5.3
fit <- rpart(Kyphosis ~ Age + Number + Start, data = kyphosis, method = "class")

summary(fit)
#> Call:
#> rpart(formula = Kyphosis ~ Age + Number + Start, data = kyphosis, 
#>     method = "class")
#>   n= 81 
#> 
#>           CP nsplit rel error   xerror      xstd
#> 1 0.17647059      0 1.0000000 1.000000 0.2155872
#> 2 0.01960784      1 0.8235294 1.058824 0.2200975
#> 3 0.01000000      4 0.7647059 1.058824 0.2200975
#> 
#> Variable importance
#>  Start    Age Number 
#>     64     24     12 
#> 
#> Node number 1: 81 observations,    complexity param=0.1764706
#>   predicted class=absent   expected loss=0.2098765  P(node) =1
#>     class counts:    64    17
#>    probabilities: 0.790 0.210 
#>   left son=2 (62 obs) right son=3 (19 obs)
#>   Primary splits:
#>       Start  < 8.5  to the right, improve=6.762330, (0 missing)
#>       Number < 5.5  to the left,  improve=2.866795, (0 missing)
#>       Age    < 39.5 to the left,  improve=2.250212, (0 missing)
#>   Surrogate splits:
#>       Number < 6.5  to the left,  agree=0.802, adj=0.158, (0 split)
#> 
#> Node number 2: 62 observations,    complexity param=0.01960784
#>   predicted class=absent   expected loss=0.09677419  P(node) =0.7654321
#>     class counts:    56     6
#>    probabilities: 0.903 0.097 
#>   left son=4 (29 obs) right son=5 (33 obs)
#>   Primary splits:
#>       Start  < 14.5 to the right, improve=1.0205280, (0 missing)
#>       Age    < 55   to the left,  improve=0.6848635, (0 missing)
#>       Number < 4.5  to the left,  improve=0.2975332, (0 missing)
#>   Surrogate splits:
#>       Number < 3.5  to the left,  agree=0.645, adj=0.241, (0 split)
#>       Age    < 16   to the left,  agree=0.597, adj=0.138, (0 split)
#> 
#> Node number 3: 19 observations
#>   predicted class=present  expected loss=0.4210526  P(node) =0.2345679
#>     class counts:     8    11
#>    probabilities: 0.421 0.579 
#> 
#> Node number 4: 29 observations
#>   predicted class=absent   expected loss=0  P(node) =0.3580247
#>     class counts:    29     0
#>    probabilities: 1.000 0.000 
#> 
#> Node number 5: 33 observations,    complexity param=0.01960784
#>   predicted class=absent   expected loss=0.1818182  P(node) =0.4074074
#>     class counts:    27     6
#>    probabilities: 0.818 0.182 
#>   left son=10 (12 obs) right son=11 (21 obs)
#>   Primary splits:
#>       Age    < 55   to the left,  improve=1.2467530, (0 missing)
#>       Start  < 12.5 to the right, improve=0.2887701, (0 missing)
#>       Number < 3.5  to the right, improve=0.1753247, (0 missing)
#>   Surrogate splits:
#>       Start  < 9.5  to the left,  agree=0.758, adj=0.333, (0 split)
#>       Number < 5.5  to the right, agree=0.697, adj=0.167, (0 split)
#> 
#> Node number 10: 12 observations
#>   predicted class=absent   expected loss=0  P(node) =0.1481481
#>     class counts:    12     0
#>    probabilities: 1.000 0.000 
#> 
#> Node number 11: 21 observations,    complexity param=0.01960784
#>   predicted class=absent   expected loss=0.2857143  P(node) =0.2592593
#>     class counts:    15     6
#>    probabilities: 0.714 0.286 
#>   left son=22 (14 obs) right son=23 (7 obs)
#>   Primary splits:
#>       Age    < 111  to the right, improve=1.71428600, (0 missing)
#>       Start  < 12.5 to the right, improve=0.79365080, (0 missing)
#>       Number < 3.5  to the right, improve=0.07142857, (0 missing)
#> 
#> Node number 22: 14 observations
#>   predicted class=absent   expected loss=0.1428571  P(node) =0.1728395
#>     class counts:    12     2
#>    probabilities: 0.857 0.143 
#> 
#> Node number 23: 7 observations
#>   predicted class=present  expected loss=0.4285714  P(node) =0.08641975
#>     class counts:     3     4
#>    probabilities: 0.429 0.571

^{Created on 2019-11-04 by the reprex package (v0.3.0.9000)}

[mdg202]

Do you perhaps know how to transform the model into one that is available to split?

[FJCC]

I would start with

model = rpart(loan_status ~ ., data=dat2, method="class")

so that all of the variables are available for splitting. You can then decrease cp if necessary but keep in mind that smaller values of cp mean making splits that are less successful in separating the classes. With 29000 observations, you should not have to adjust minsplit and minbucket.