How to find the minimum slope in a curve

[rhesus]

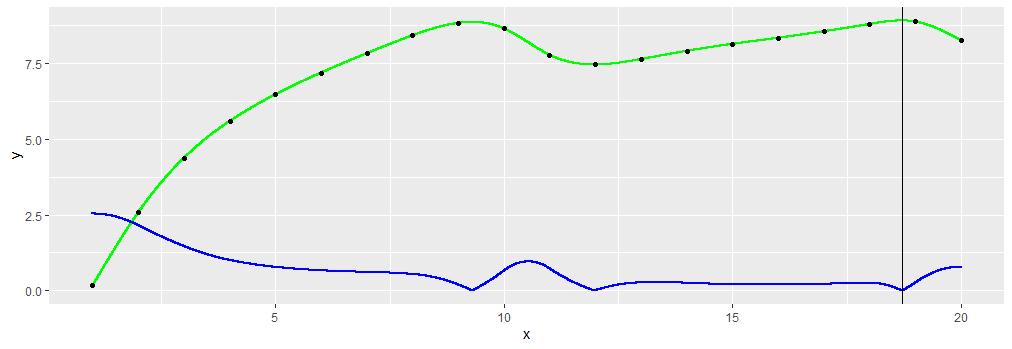
I have graphed a dataframe and got this asymptote. How can I go about finding the point where the curve starts to plateau? That is, the minimum slope, I think.

[nirgrahamuk]

I think it would be something along these lines

library(tidyverse)

example_data <- structure(list(x = c(1:40), y = c(
  0.165, 2.572,
  4.365, 5.576, 6.456, 7.173, 7.811, 8.399, 8.811, 8.631, 7.761,
  7.443, 7.619, 7.89, 8.12, 8.321, 8.535, 8.773, 8.858, 8.248,
  6.821, 6.163, 6.172, 6.321, 6.433, 6.52, 6.631, 6.779, 6.761,
  5.967, 4.264, 3.442, 3.383, 3.489, 3.556, 3.588, 3.613, 3.638,
  3.663, 3.689
)), class = "data.frame", row.names = c(NA, -40L))%>% slice(1:20)

model <- smooth.spline(x = example_data$x, y = example_data$y)
more_x <- seq(from=1,to=20,length=8000)
Y <- predict(model, x = more_x, deriv = 1) # first derivative
Yo <- predict(model, x = more_x, deriv = 0) # original
(deriv_data <- tibble(data.frame(Y))  %>% 
    mutate(abs_y=abs(y)))
(smooth_data <- tibble(data.frame(Yo)))
(x_of_min_deriv <- deriv_data$x[which.min(deriv_data$abs_y)])  

ggplot() + 
  geom_point(data=smooth_data,
           aes(x,y),color="green",size=.1) +
geom_point(data=example_data,
       aes(x,y)) +
  geom_point(data=deriv_data,
             aes(x,abs_y),color="blue",size=.1) +
  geom_vline(xintercept = x_of_min_deriv)

Edited to also show the initial smooth.spline in green

[arthur.t]

That is exactly how I would do it. Smoothing splines is a great way to estimate the derivative of data.

[Yarnabrina]

While nirgrahamuk absolutely answered the question in the title (assuming degrees of splines are not of concern), I feel OP is mainly interested in finding the "elbow" (or knee) point, and I'm not convinced that it corresponds to minimum slope of curve.

[nirgrahamuk]

I do agree that finding the 'knee of the curve' is a different question to the one I chose to answer.
I found this material : (PDF) Reliable computations of knee point for a curve and introduction of a unit invariant estimation (researchgate.net)
It includes R code in the appendix !

[rhesus]

I thought the minimum slope was the same point that the knee of the curve, my fault.
Thank you so much for your answers, the code and the material!

[fcas80]

Here is my attempt at a knee. This is based on https://www.datasciencecentral.com/how-to-automatically-determine-the-number-of-clusters-in-your-dat/ , except I am allowing positive or negative strength.

library(dplyr)
x <- seq(from=1, to=40)
y = c(
0.165, 2.572,
4.365, 5.576, 6.456, 7.173, 7.811, 8.399, 8.811, 8.631, 7.761,
7.443, 7.619, 7.89, 8.12, 8.321, 8.535, 8.773, 8.858, 8.248,
6.821, 6.163, 6.172, 6.321, 6.433, 6.52, 6.631, 6.779, 6.761,
5.967, 4.264, 3.442, 3.383, 3.489, 3.556, 3.588, 3.613, 3.638,
3.663, 3.689)
df <- data.frame(cbind(x,y))
df$delta1 <- lag(df$y) - df$y
df$delta2 <- round(lag(df$delta1) - df$delta1,2)
df$strength <- ifelse(!is.na(lead(df$delta2) - lead(df$delta1)) , lead(df$delta2) - lead(df$delta1), NA)
head(df,10)
m <- max(abs(df$strength), na.rm=TRUE)
m
w <- which(df$strength == m | df$strength == -m)
w
plot(x,y,"b", col="black", lwd=2)
abline(v=w, col="black", lwd=5)

x     y delta1 delta2 strength

1 1 0.165 NA NA NA
2 2 2.572 -2.407 NA 1.183
3 3 4.365 -1.793 -0.61 0.631
4 4 5.576 -1.211 -0.58 0.550
5 5 6.456 -0.880 -0.33 0.557
6 6 7.173 -0.717 -0.16 0.558
7 7 7.811 -0.638 -0.08 0.538
8 8 8.399 -0.588 -0.05 0.232
9 9 8.811 -0.412 -0.18 -0.770
10 10 8.631 0.180 -0.59 -1.560
[1] 2.613
[1] 30

[rhesus]

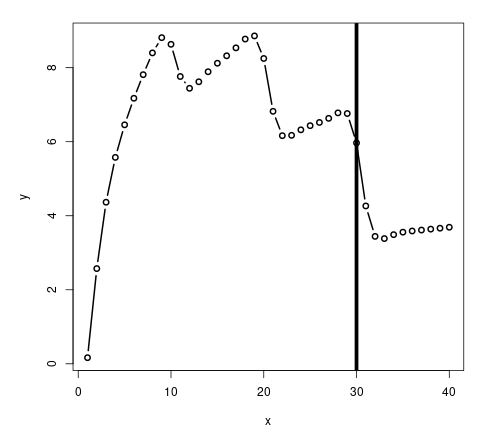
Thank you so much, this is very helpful for me.