Points Appearing in Graph that are Not in the Dataset

[omario]

I am working with the R programming language.

I tried to plot the Likelihood Function of a Normal Distribution:

library(plotly)
y <- rnorm(5,5,5)

my_function <- function(x1,x2) {
    
    n = 20
    
    a = n/2*log(2*pi)
    b = n/2*log(x2^2)
    c = 1/(2*x2^2)
    d = sum ((y-x1)^2)    
    return (a + b + c* d)
    
}
input_1 <- seq(1, 10,0.1)
input_2 <- seq(1, 10,0.1)


z <- outer(input_1, input_2, my_function)

plot_ly(x = input_1, y = input_2, z = z) %>% add_surface()

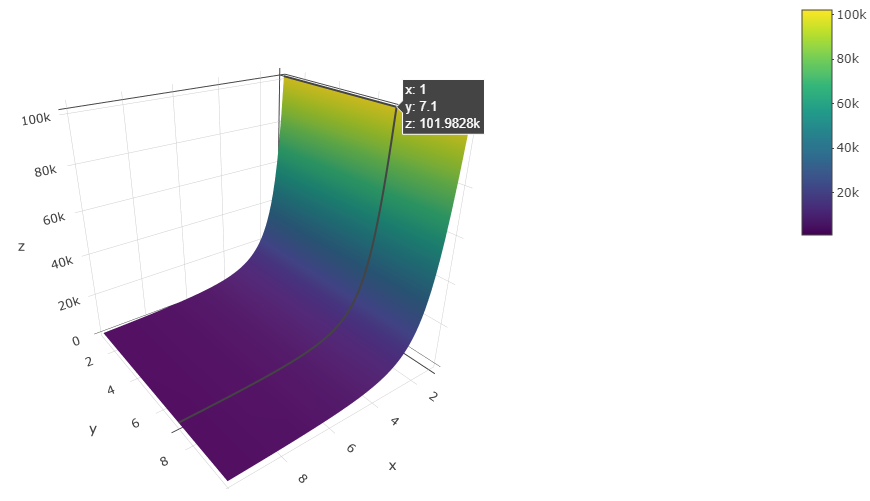
As we can see here, there some values on this graph that are close to 100,000:

However, over the range at which this function was evaluated, the function can never take such a large value. For example, if I were to evaluate this function at the same point that appears in the above picture, I get a value that is nowhere close to 100,000

my_function(1, 7.1) 
[1] 59.94714

Have I plotted this function correctly? Why does the value in the picture not match with the value I get from manually evaluating the function? Can someone please explain why this is happening and what I can do to fix this problem?

Thanks!

Note:

• From a mathematics and statistics perspective, I don't think it is possible for the Likelihood Function of a Normal Distribution (for a small dataset generated from a Normal Distribution of mean = 5 and standard deviation = 5) could take such large values (Likelihood function - Wikipedia)
• I think the problem in this question is related to the outer() function - I don't think the correct values of the function are being calculated via the outer() function (e.g. take for instance the discrepancy between 59.9 vs 120,000)

[FJCC]

I think this version of your function gets you what you want. The key is that my_function gets the entire vectors input_1 and input-2, so x1 is not a value from input_1, it is the entire vector. In your version of the function, that makes y - x1 the difference between the 5-vector y and the 91-vector x1.

set.seed(123)
y <- rnorm(5,5,5)

my_function <- function(x1,x2) {
  n = 20
  a = n/2*log(2*pi)
  b = n/2*log(x2^2)
  c = 1/(2*x2^2)
  d1 <- (y[1]-x1)^2
  d2 <- (y[2]-x1)^2
  d3 <- (y[3]-x1)^2
  d4 <- (y[4]-x1)^2
  d5 <- (y[5]-x1)^2
  d <- d1+d2+d3+d4+d5
  #d = sum ((y-x1)^2)    
  tmp <- a + b + c* d
  return (tmp)
  
}
input_1 <- seq(1, 10,0.1)
input_2 <- seq(1, 10,0.1)
z <- outer(input_1, input_2, my_function)
my_function(1,1)
#> [1] 112.9655
z[1,1]
#> [1] 112.9655

^{Created on 2022-03-27 by the reprex package (v2.0.1)}

[omario]

Thank you so much! This seems to have worked!