Hi, John, and welcome to the RStudio Community!
I've been trying to muster the time needed to write a better answer, but alas, without success. Following Voltaire's maxim that the best is enemy of the good, here is a sub-optimal answer ![]() I'll leave it to someone else to touch decision trees & GBMs, since I don't know about the use of cross-validation to estimate the variable importance for these models. For decision trees, you may have a look here: it's actually about the generalization error (see below), but it might contain useful references (or you may ask the author).
I'll leave it to someone else to touch decision trees & GBMs, since I don't know about the use of cross-validation to estimate the variable importance for these models. For decision trees, you may have a look here: it's actually about the generalization error (see below), but it might contain useful references (or you may ask the author).
Re: ROC curves. What would you like to learn from the 10 different ROC curves? If you're trying to compute confidence intervals for the ROC curve, then using the 10 ROC curves is not a rigorous approach (i.e., there's no proof they'll converge to the right confidence intervals). You can at most consider them as an estimate of how sensitive the classifier is to the training set. See for example here for some Python code: you could of course do the same in R. Two caveats:
- you can only do this if the classified outputs probabilites, rather than simply classes (but I'm sure you know this already)
- as the validation sets get smaller, this procedure becomes more and more dubious. For example, for leave-one-out cross-validation, each of the N ROC curves would be computed based on a single test point...thus the variance of the estimator would be pretty large.
In general, cross-validation is introduced because the training error, i.e., the error of the learned model on the training set:

is usually an optimistic estimate of the test error, also called generalization error or out-of-sample error:
![]()
i.e., the average over all learnable models (in our hypothesis class) of the average error over all possible test sets1. When we say that it's a optimistic estimate, we mean that the difference
![]()
called the optimism, is often larger than 0.
A better estimate of the test error is the K-fold cross-validation error:
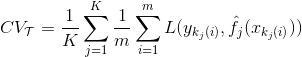
The notation is a bit complicated, but the concept is simple:
- split our dataset T, of size N, in K parts of size m
- fit your model K times to training sets of size N-m, each obtained by removing one split of size m from T, and each time compute the error on the hold-out set
- average the K errors together
Thus, usually the cross-validation error is used as an estimate of the test error. Starting from here, you can of course also use it as an heuristic for all sort of statistical decisions, such as for example model selection. But it's just that - an heuristic. You're not sure it will always work. For example, for model selection, it's well known that, if the true model belongs to the class of models you can learn with your learning algorithm, then neither LOOCV or leave-K-out cross-validation (a form of cross-validation where you test on all possible folds of size K) are consistent, i.e., they won't select the true model as N goes to infinity (though leave-K-out cross-validation becomes consistent, if K increases sufficiently fast with N). You may argue that consistency is not necessarily an interesting/desirable property, because for many practical case we don't know whether the true model belongs to our hypothesis space or not. That's true. But, for many practical cases, we don't even know how much less optimistic the cross-validation error is, with respect to the test error. For a review of what theory actually tells us about cross-validation, see
1We would be actually more interested in estimating the conditional test error, i.e., the average error of our learned model over all possible test sets
![]()
but I don't think efficient estimates of this error are currently known.