Changing axis labels without changing the plot (ggplot)

[Dutchottie]

Hi,
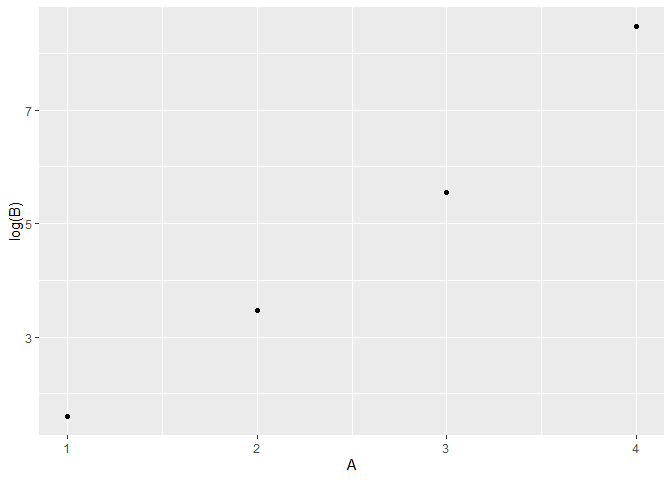
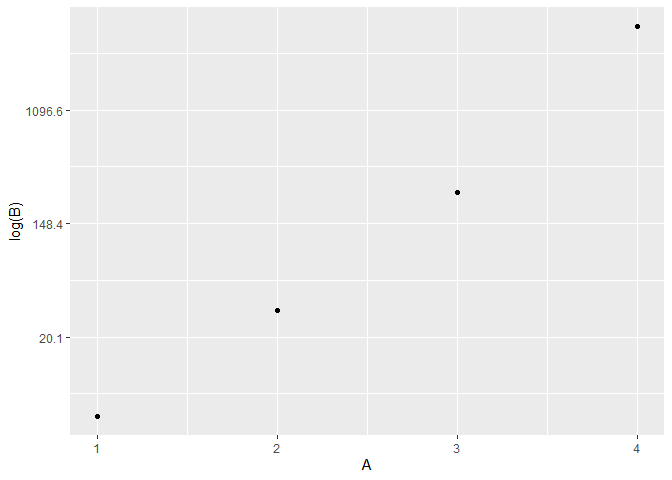
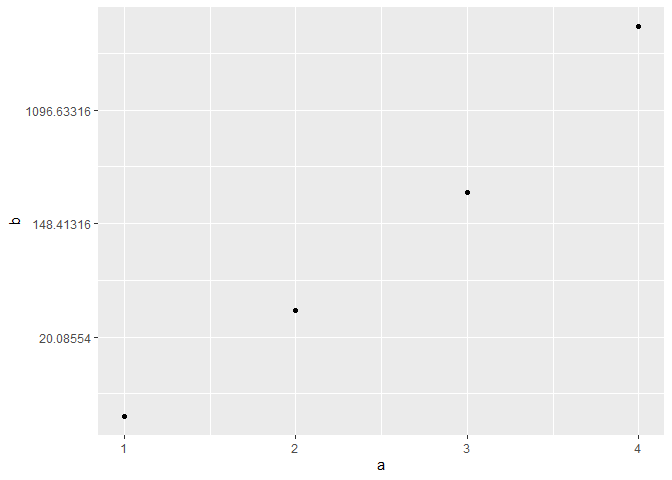
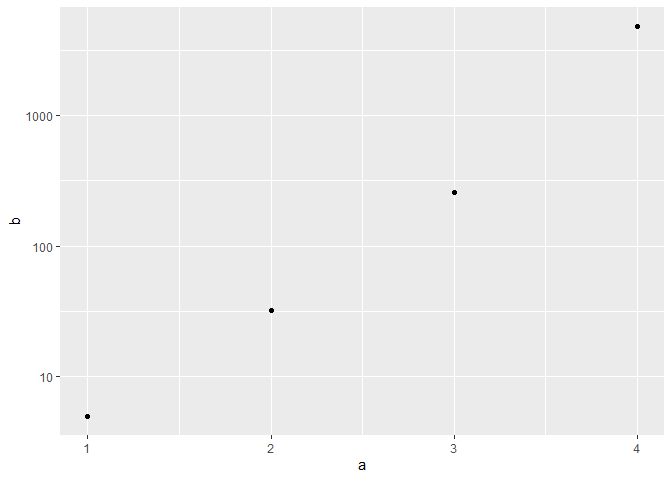
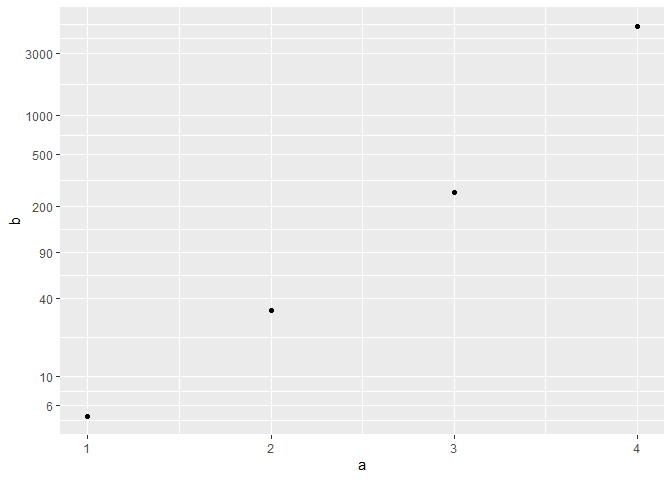
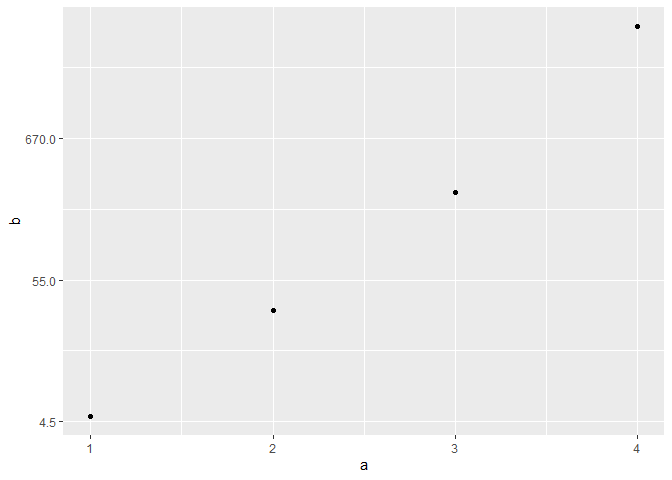
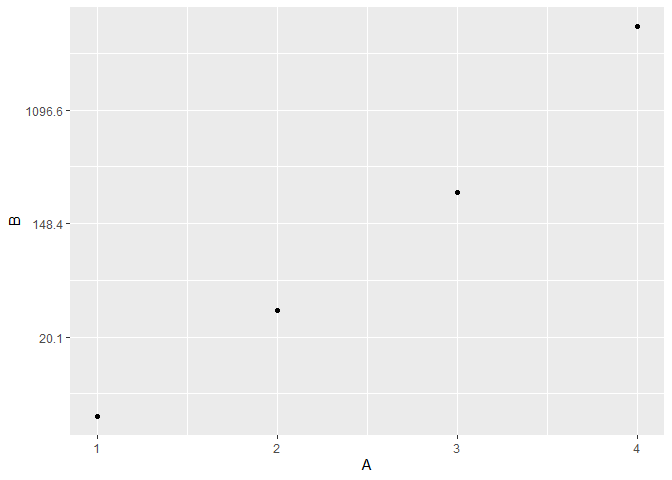
I've got a ggplot that uses log(x) for the y-axis. Y values ranging from >0 to <20,000 so log(y) roughly between -10 and +10.
What I want is to use the log(y) values to plot, but to use the (raw) Y values for the y-axis labels.

I've looked at the ggplot2 options and the scales package, but for the life of me I can't seem to get it working. Any suggestions?

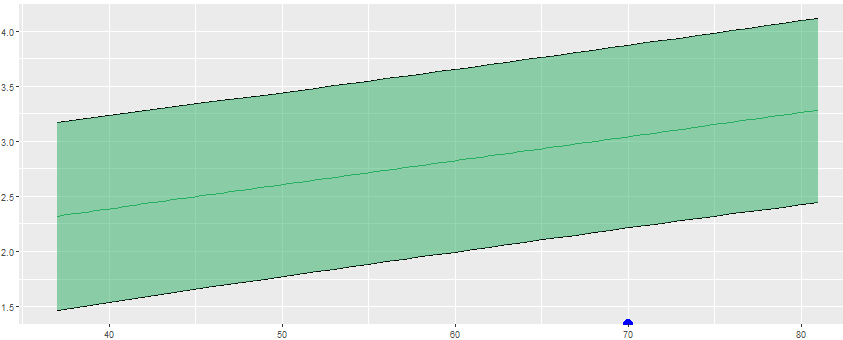
This is my ggplot command (with the default log(y) labels):

tryCatch(
		{	#This is the Try section
			plotthis <- toplot() #Get the data to plot

	        p <- ggplot(data = plotthis, aes(x = age, y = nfl, fill = diagnosis)) + #init the plot object and (aestatically) map (aes) the data to internal variables x and y
	        	#prediction interval
	            geom_line(aes(y=lwr, linetype = diagnosis)) + #draw lower prediction interval line - remove linetype here and set to ggplot aes to also change the regres linetype
	    		geom_line(aes(y=upr, linetype = diagnosis)) + #draw higher prediction interval line
	    		geom_ribbon(aes(ymin = lwr, ymax = upr, fill = diagnosis), alpha = 0.5) +  #"grey70"
	    		#regression line
	            geom_smooth(aes(color = diagnosis), method=lm, se=FALSE, size = 0.5) + #show regression line with confidence area
	            #overrides
	    		scale_color_manual(values = line_colors) +
				scale_linetype_manual(values = line_types) +
	    		scale_fill_manual(values = fill_colors) +
	            #patient info
	            geom_point(aes(x=input$patient_age, y=log(input$patient_nfl), size = 3), colour="blue") + #add the patient point
	            #layout
	            xlab(xlab) +
	            ylab(ylab) +
	            guides(colour = guide_legend("Selected diagnosis"), fill = guide_legend("Selected diagnosis"), linetype = guide_legend("Selected diagnosis")) +
	            guides(size = FALSE) + #remove size (dot) from legend
	            xlim(adjusted_minx(),adjusted_maxx()) + #set x axis range
	            theme(legend.position = "bottom")
	            plot(p)
    	},
		error=function(cond){
			showNotification("Invalid combination of choices. Resetting interface.", type = "error", closeButton = TRUE)
	    	#message(cond)
	    	resetall()
	    	# Choose a return value in case of error
	    	return(NA)
		},
		finally={
	        #message("Some other message at the end")
		}
		)
	})

[FJCC]

Here are some simple examples of plotting the log of a value on the y axis and labeling the axis in different ways. The first plot should be similar to what you are getting, the second uses the scale_y_log10() function to automatically label with the raw values but using base 10, and the third manually labels with the powers of e.

library(ggplot2)
DF <- data.frame(A = 1:4, B = c(5, 32, 256, 4781))

#Default labels with powers of e
ggplot(DF, aes(A, log(B))) + geom_point()

#Use scale_y_log10()
ggplot(DF, aes(A, B)) + geom_point() + 
  scale_y_log10()

#Manual labels ploting log(B) but labeling with raw values
ggplot(DF, aes(A, log(B))) + geom_point() + 
  scale_y_continuous(breaks = c(3,5,7), 
                     labels = round(c(exp(3), exp(5), exp(7)), 1))

^{Created on 2020-09-01 by the reprex package (v0.3.0)}

[elmstedt]

The solutions provided by @FJCC will work quite well, especially if you are plotting this sort of thing as a one-off visualization. If, however, you find yourself doing many of these types of plots, you might want to think first about employing the transformation abilities of the scale_y_ and scale_x_ functions, then later you can craft your own to fine tune the results.

First our data:

library(ggplot2)
df <- data.frame(a = 1:4, b = c(5, 32, 256, 4781))

Using trans =

We can choose a transformation function for our axis using the trans argument. Per the help file ?scale_y_continuous we have access to several pre-made transformations,

Built-in transformations include "asn", "atanh", "boxcox", "date", "exp",
"hms", "identity", "log", "log10", "log1p", "log2", "logit", "modulus",
"probability", "probit", "pseudo_log", "reciprocal", "reverse", "sqrt" and "time".

and in your case using trans = "log" works quite well,

ggplot(df, aes(a, b)) +
  geom_point() + 
  scale_y_continuous(trans = "log")

NOTE: If you used trans = "log10" this results in a plot identical to using scale_y_log10()` as in the second example from FJCC.

ggplot(df, aes(a, b)) +
  geom_point() + 
  scale_y_continuous(trans = "log10")

Having more control

Now that we've seen we can set a transformation on the y scale, we can extend that and make our own. We do that with the trans_new() function in the scales package.

The usage of trans_new() looks like this,

trans_new(name,
          transform,
          inverse,
          breaks = extended_breaks(),
          minor_breaks = regular_minor_breaks(),
          format = format_format(),
          domain = c(-Inf, Inf))

Custom Breaks Fucntion

Since we are interested in where the breaks fall, we can consider writing a custom breaks function.

# We will use the default breaks function from trans_new()
# as a template to build our new breaks function
scales::extended_breaks
#> function (n = 5, ...) 
#> {
#>     n_default <- n
#>     function(x, n = n_default) {
#>         x <- x[is.finite(x)]
#>         if (length(x) == 0) {
#>             return(numeric())
#>         }
#>         rng <- range(x)
#>         labeling::extended(rng[1], rng[2], n, ...)
#>     }
#> }
#> <bytecode: 0x000000001a7e6298>
#> <environment: namespace:scales>

# the idea is to,
# compute the log of our response
# find attractive break points
# resolve the values back to their original scale

logexp_breaks <- function (n = 5, sigdig = 2, ...) {
  n_default <- n
  function (x, n = n_default) {
    x <- x[is.finite(x)]
    if (length(x) == 0) {
      return(numeric())
    }
    rng <- range(log(x))
    breaks <- labeling::extended(rng[1],
                                 rng[2],
                                 n,
                                 ...)
    signif(exp(breaks), sigdig)
  }
}

Custom Transformation Function

Now that we have the breaks function written which our transformation function will use we can start on the transformation.

We'll base our custom transformation function on log_trans(), so let's look at the code before we get started.

# 
scales::log_trans
#> function (base = exp(1)) 
#> {
#>     force(base)
#>     trans <- function(x) log(x, base)
#>     inv <- function(x) base^x
#>     trans_new(paste0("log-", format(base)), trans, inv, log_breaks(base = base), 
#>         domain = c(1e-100, Inf))
#> }
#> <bytecode: 0x0000000019bdac98>
#> <environment: namespace:scales>

Now, in exploring, I thought it would be good to allow our transformer to take some arguments and send them along to our breaks function. We could have sent some args to the actual transformation and inverse as seen in the log_trans() example, but I wanted to keep this simple_-ish_, so we'll just let elm() accept the three dots and pass them straight on through to logexp_breaks(). The parameters of interest for the breaks function will be n (a rough guide for how many major breaks to make), sigdig (the number of significant digits to set our breaks at), and w (the weights to pass on to the labeling function which does the heavy lifting about where to set the breaks).

NOTE: The weights are a bit of a mystery to me. The help file ?labeling::extended has this to say about them,

w         weights applied to the four optimization components (simplicity,
          coverage, density, and legibility)

You should play around with them to find a balance you like (or just trust the default).

elm <- function(...) {
  scales::trans_new("elm",
                    "log",
                    "exp",
                    logexp_breaks(...))
}

Putting it into practice.

Now that we've done all that, we can start to put it into practice and see what we get.

ggplot(df, aes(a, b)) +
  geom_point() + 
  scale_y_continuous(trans = elm(n = 10, sigdig = 1, w = c(0.01, 0.1, 0.7, 0.05)))

ggplot(df, aes(a, b)) +
  geom_point() + 
  scale_y_continuous(trans = elm(n = 4, sigdig = 2))

^{Created on 2020-09-01 by the reprex package (v0.3.0)}

[elmstedt]

@FJCC

ggplot(DF, aes(A, log(B))) + geom_point() + 
  scale_y_continuous(breaks = c(3,5,7), 
                     labels = round(c(exp(3), exp(5), exp(7)), 1))

The problem with this is the axis is labelled log(B) but the value labels are in terms of B. This would be a very confusing plot for me. I think you need to update the ylab to ensure the label and the values match,

library(ggplot2)
DF <- data.frame(A = 1:4, B = c(5, 32, 256, 4781))
ggplot(DF, aes(A, log(B))) + geom_point() + 
  scale_y_continuous(breaks = c(3,5,7), 
                     labels = round(c(exp(3), exp(5), exp(7)), 1)) +
  ylab("B")

^{Created on 2020-09-01 by the reprex package (v0.3.0)}

[Dutchottie]

Thanks all!
Unfortunately I'm still running into a problem.
My graph uses data that is already transformed into ln(value) [with the log() function].
I need the natural logarithm to calculate the regression line and the prediction boundaries, using the geom_line & _ribbon &_smooth() functions.
I want to display the non-ln() values (ie the raw values) on the y-axis. However, when I use:
scaly_y_continuous(trans = "exp") R pops an error:

Warning: Transformation introduced infinite values in continuous y-axis
geom_smooth() using formula 'y ~ x'
Warning in self$trans$inverse(limits) : NaNs produced

If I leave the "trans="exp"" out of the scale command, there's no error.

I don't understand why the addition of the trans command would suddenly produce infinite values that are not there in my data nor in the graph when not using the trans command.

Anyone have any ideas why this does not work?

Thanks!
Marco

[elmstedt]

@Dutchottie

I don't understand why the addition of the trans command would suddenly produce infinite values that are not there in my data nor in the graph when not using the trans command.

Because you are transforming the data a second time. It would be better if you simply plotted your raw data and handled the transformation in the scale function.

[Dutchottie]

Yes, I understand that would be easier if you need to manage the y-axis. However, the only way I got my graph to plot what I want is to combine my data and my predict model into one data frame. And I need the ln() values of my data to do the lm and subsequently the predict calculations.
But if my data set is raw (ie not ln-values of the raw) and my lm & predict need ln-values to get the right regression and prediction, how do I combine these into a sensible graph (see screen shot)?
Plus my x and y values depend on the selection the user makes (I'm using Shiny to visualize), so I can't fix them in any way.

I think I'm confused!