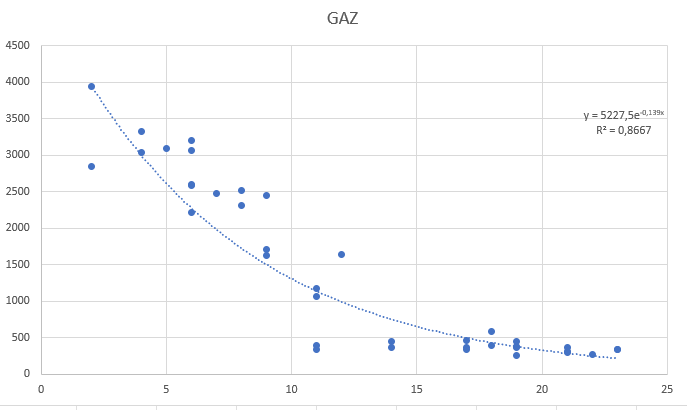
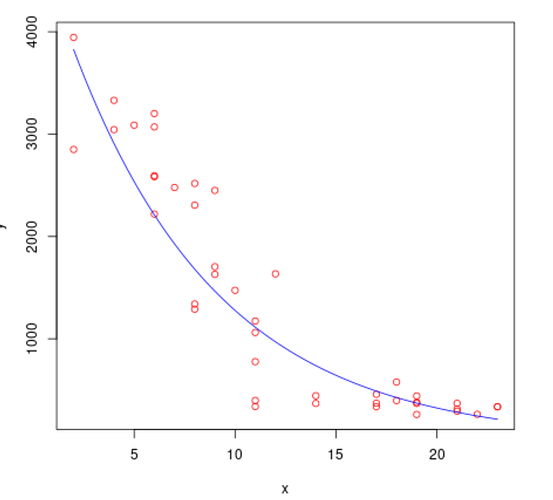
I want to do an exponential regression with this data in order to compare with linear and polynomial model.
TEMPERATURE;GAZ
8;1290
8;1340
10;1474
11;777
18;397
22;263
21;370
18;578
14;444
7;2478
6;3201
4;3330
8;2518
8;2306
12;1635
14;369
17;458
21;315
23;336
19;442
11;1062
9;2450
5;3088
2;3945
6;3070
6;2594
9;1705
11;398
19;369
19;261
19;379
17;371
11;339
6;2219
4;3044
2;2850
6;2584
9;1630
11;1174
17;337
21;293
23;337
My results for the linear model :
Call:
lm(formula = GAZ ~ TEMPERATURE, data = edf)
Residuals:
Min 1Q Median 3Q Max
-1251.29 -278.31 84.01 364.99 919.76
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3344.1 183.3 18.25 < 2e-16 ***
TEMPERATURE -159.4 13.4 -11.90 1.02e-14 ***
Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 538.7 on 40 degrees of freedom
Multiple R-squared: 0.7797, Adjusted R-squared: 0.7742
F-statistic: 141.6 on 1 and 40 DF, p-value: 1.021e-14
My results for the polynomial model :
lm(formula = GAZ ~ TEMPERATURE + I(TEMPERATURE^2), data = edf)
Residuals:
Min 1Q Median 3Q Max
-1026.93 -82.48 40.43 135.98 798.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4706.316 279.455 16.841 < 2e-16 ***
TEMPERATURE -436.194 50.380 -8.658 1.28e-10 ***
I(TEMPERATURE^2) 10.752 1.917 5.607 1.82e-06 ***
Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 406 on 39 degrees of freedom
Multiple R-squared: 0.878, Adjusted R-squared: 0.8718
F-statistic: 140.4 on 2 and 39 DF, p-value: < 2.2e-16
GRAPHIQUE.pdf (8.4 KB)