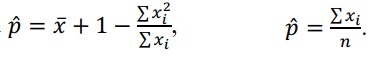Monte Carlo simulations for binomial distribution

[Alexander_dos_Santos]

Hey guys. I'm new to R so I need a little help

I'm trying to check if the estimators that I'm using for a binomial distribution parameter actually tends to the actual one through a Monte Carlo simulation with 10k replications.

For that I'm basing my code in one that I found for the exponential one. First, I wanna understand the code. So here it is:
........................................................................................................................

#This file is a Monte Carlo study of the small sample
#behaviour of the sample mean estimators of the Expected value.
#and the power and size of the associated test statistics.

1000 REPLICATIONS, SAMPLE SIZES 1000, 200, 20 10

Rp<-10000 # no.of replications
sz <-1000 # sample size
#resulting matrices
TT<-matrix(0,ncol=4,nrow=Rp) # estimates matrix
TS<-matrix(0,ncol=4,nrow=Rp) # Std Err. matrix

#Simulation
for(i in 1:Rp) {
X<-rexp(sz,rate=2)
#mean estimates
TT[i,1]<-1/mean(X) #1 #equation1
TS[i,1]<-1/mean(X)^2/sz #2 #equation2
#mean estimates
TT[i,2]<-1/mean(X[c(1:200)]) #3
TS[i,2]<-(1/mean(X[c(1:200)])^2)/(200) #4
#mean estimates
TT[i,3]<-1/mean(X[c(1:20)]) #5
TS[i,3]<-(1/mean(X[c(1:20)])^2)/(20) #6
#mean estimates
TT[i,4]<-1/mean(X[c(1:10)]) #7
TS[i,4]<-(1/mean(X[c(1:10)])^2)/(10) #8
}

#bias and efficiency
#sample mean
summary(TT[,1])
summary(TT[,2])
summary(TT[,3])
summary(TT[,4])

...........................................................................................................................

I understand that it's being repeated 10k times, so each time he generates a different X, base on the sample size and the rate, to use #equation1 to estimate my parameter [E(x)] in #1. So in the column 1 of the matrix TT, is being stored those estimations. Similar thing being done for the #equation2, but for the variance estimation.

But on #3 , what does the c(1:200) means? does it means that from the sample size of 1000, hes only using 200 of those? So in that case I dont need to change the sample size, SZ, to know the estimation for different sample sizes (100,20 and 10)?

[nirgrahamuk]

yes, and correct.
we can reduce the repetition in the code by use of functions that will perform variations on the same repeated calculation, and gain more flexibility of the sample sizes per replications like so:

Rp<-10000 # no.of replications
sz <-c(1000,200,100,10) # sample sizes
#resulting matrices
TT<-matrix(0,ncol=4,nrow=Rp) # estimates matrix
TS<-matrix(0,ncol=4,nrow=Rp) # Std Err. matrix

mean_estimates <- function(X, n) {
  c( 1 / mean(X[c(1:n)]),
    (1 / mean(X[c(1:n)])^2) / (n))
}

#Simulation
for(i in 1:Rp) {
  X<-rexp(sz[[1]],rate=2)
  #mean estimates
  for(j in seq_along(sz)){
    res <- mean_estimates(X,sz[j])
  TT[i,j]<- res[[1]]
  TS[i,j]<- res[[2]]
  }
}

[Alexander_dos_Santos]

Thank you very much for the reply, @nirgrahamuk .

I have a few questions.

I did search for the meaning of [[1]] - both for sz[[1]] and res[[1]] -, but I did not understand. I know what "res" is, since it is defined. I assume it's merely the results of the function you defined, which would be the estimators for my exp distribution. Does the " res[[1]] " means that hes doing the results for the first equation attributed to the variable mean_estimates? So the " res[[2]] " would be the results for the second equation defined?

In any case, since I'm doing that for binomial, I tried to rewrite and it worked. Except for the fact that the TT matrix and TS matrix have exactly the same values. Ignore the name of the matrices, since for exp I was trying to estimate something a bit different.

Before the code, let me explain what I'm doing.

As I said I'm trying to check if the estimators that I'm using for "p" of my binomial distribution tends the actual "p". For that my estimators are

with "n" being the sample size, and N, number of trials, being 1 and the real value of "p" being 2/3.

Heres the code:

---

Rp<-10000 # no.of replications
sz <-c(1000,200,100,10) # sample sizes
#resulting matrices
TT<-matrix(0,ncol=4,nrow=Rp) # estimates matrix
TS<-matrix(0,ncol=4,nrow=Rp) # Std Err. matrix

mean_estimates <- function(X, n) {
c( mean(X[c(1:n)]) +1 - (sum(X[c(1:n)]^2)) / (sum(X[c(1:n)])),
sum(X[c(1:n)]) / n)
}

#Simulation
for(i in 1:Rp) {
X<-rbinom(sz[[1]],1, 2/3)
#mean estimates
for(j in seq_along(sz)){
res <- mean_estimates(X,sz[j])
TT[i,j]<- res[[1]]
TS[i,j]<- res[[2]]
}
}
summary(TT[,1])
summary(TT[,2])
summary(TT[,3])
summary(TT[,4])

summary(TS[,1])
summary(TS[,2])
summary(TS[,3])
summary(TS[,4])

---

Am I doing something wrong? I'm almost sure the results for both the equations shouldnt be the same. Maybe approximate, but not the same.

[nirgrahamuk]

the issue is because of your inputs.
the equations do work out to be the same given that with rbinom your inputs are either 0 or 1, i.e. the square of 0 and of 1 are 0 and 1, therefore squaring the values is no different to not squaring them.

[Alexander_dos_Santos]

Oh, thank you again

If I put a different number of trials, it does give different values. So the code is working just fine.