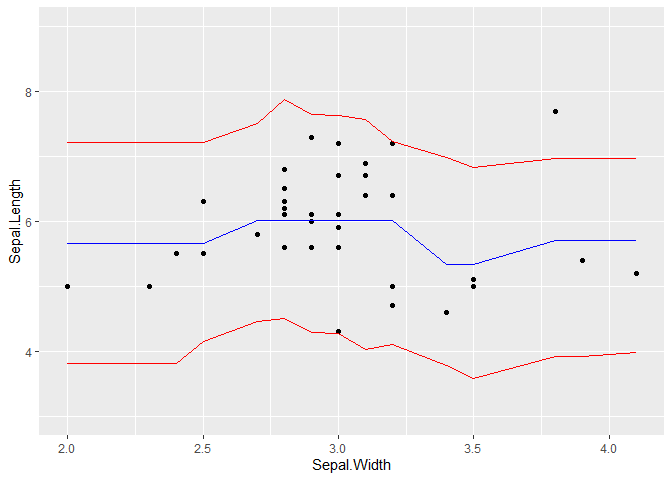
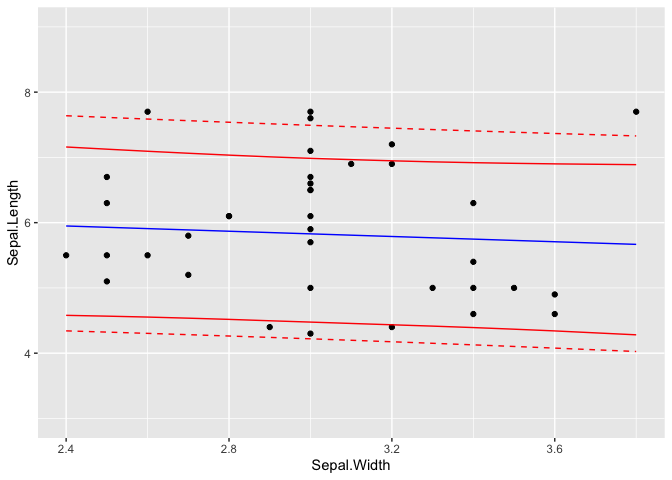
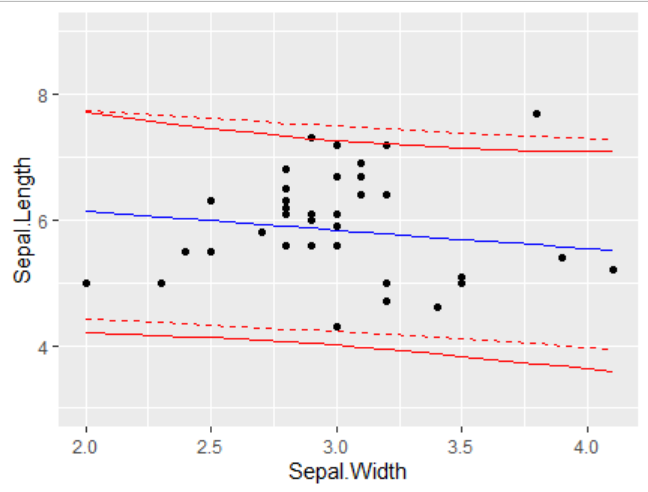
What is the best practice for producing prediction intervals (not confidence intervals) for predictions using tidymodels (would prefer genralizable approach or at least across more than just linear regression and use of simulation methods when appropriate).
I read through these: https://github.com/tidymodels/parsnip/search?q=prediction+intervals&type=issues -- but got a little lost as seemed like was rolled into parsnip::predict() but also doesn't seem to have full set of features disucssed by Alex Hayes
Max in initial discussion... I was unclear exactly if this exists somewhere or will exist in the future.
I'm also interested if there are any good tidy tutorials out there on prediction intervals already that use existing tools (e.g. that take advantage of rsample, broom, etc).
(Link to helpful blog that breaks down sources of noise for bootstrapping prediction intervals: https://saattrupdan.github.io/2020-03-01-bootstrap-prediction/ , but code examples are in python).
This question was posted previously on the R4DS Online Learning Community Slack channel: https://rfordatascience.slack.com/archives/C8JSHANJY/p1601014414012500